| << Chapter < Page | Chapter >> Page > |
Conservation of energy includes rotational motion, because rotational kinetic energy is another form of . Uniform Circular Motion and Gravitation has a detailed treatment of conservation of energy.
One of the quality controls in a tomato soup factory consists of rolling filled cans down a ramp. If they roll too fast, the soup is too thin. Why should cans of identical size and mass roll down an incline at different rates? And why should the thickest soup roll the slowest?
The easiest way to answer these questions is to consider energy. Suppose each can starts down the ramp from rest. Each can starting from rest means each starts with the same gravitational potential energy , which is converted entirely to , provided each rolls without slipping. , however, can take the form of or , and total is the sum of the two. If a can rolls down a ramp, it puts part of its energy into rotation, leaving less for translation. Thus, the can goes slower than it would if it slid down. Furthermore, the thin soup does not rotate, whereas the thick soup does, because it sticks to the can. The thick soup thus puts more of the can's original gravitational potential energy into rotation than the thin soup, and the can rolls more slowly, as seen in [link] .
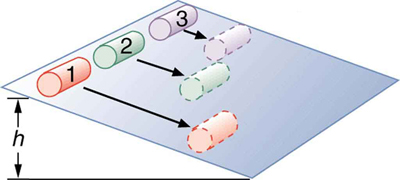
Assuming no losses due to friction, there is only one force doing work—gravity. Therefore the total work done is the change in kinetic energy. As the cans start moving, the potential energy is changing into kinetic energy. Conservation of energy gives
More specifically,
or
So, the initial is divided between translational kinetic energy and rotational kinetic energy; and the greater is, the less energy goes into translation. If the can slides down without friction, then and all the energy goes into translation; thus, the can goes faster.
Locate several cans each containing different types of food. First, predict which can will win the race down an inclined plane and explain why. See if your prediction is correct. You could also do this experiment by collecting several empty cylindrical containers of the same size and filling them with different materials such as wet or dry sand.
Calculate the final speed of a solid cylinder that rolls down a 2.00-m-high incline. The cylinder starts from rest, has a mass of 0.750 kg, and has a radius of 4.00 cm.
Strategy
We can solve for the final velocity using conservation of energy, but we must first express rotational quantities in terms of translational quantities to end up with as the only unknown.
Solution
Conservation of energy for this situation is written as described above:
Before we can solve for , we must get an expression for from [link] . Because and are related (note here that the cylinder is rolling without slipping), we must also substitute the relationship into the expression. These substitutions yield
Interestingly, the cylinder's radius and mass cancel, yielding
Solving algebraically, the equation for the final velocity gives
Substituting known values into the resulting expression yields
Discussion
Because and cancel, the result is valid for any solid cylinder, implying that all solid cylinders will roll down an incline at the same rate independent of their masses and sizes. (Rolling cylinders down inclines is what Galileo actually did to show that objects fall at the same rate independent of mass.) Note that if the cylinder slid without friction down the incline without rolling, then the entire gravitational potential energy would go into translational kinetic energy. Thus, and , which is 22% greater than . That is, the cylinder would go faster at the bottom.

Notification Switch
Would you like to follow the 'College physics for ap® courses' conversation and receive update notifications?